Общая последовательность изучения материала линии неравенств
В третью группу входят наглядно-графические приемы. Большинство этих приемов используют в качестве основы координатную прямую либо координатную плоскость.
Использование координатной прямой позволяет решать некоторые неравенства и системы неравенств с одним неизвестным, а также неравенства с модулями. Например, прием решения систем линейных неравенств с одним неизвестным состоит в том, что на координатную прямую наносятся множества решений каждого неравенства, а потом выделяется их общая часть. Решение уравнений и неравенств с модулями связывается с геометрической интерпретацией модуля разности чисел.
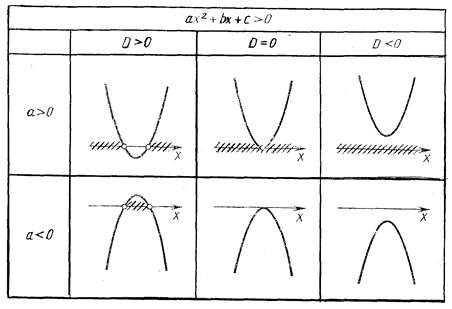
Использование координатной плоскости позволяет применить графические методы к решению и исследованию неравенств и их систем как с одним, так и с двумя неизвестными. Графические приемы эффективно применяются для изображения результатов исследования там, где чисто аналитическая запись громоздка. Характерным примером служит схема, на которой приведены различные случаи решения неравенства ax²+bx+c>0, помещенная на рис.3. В результате определенной тренировки учащиеся привыкают пользоваться такой схемой, а затем ее мысленным образом.
Еще по теме:
Понятие, цели и задачи краеведения в школе
Для того чтобы рассмотреть краеведение как элемент исторического образования необходимо сначала разобраться с самим понятием. Большая Советская энциклопедия дает, как мне кажется, самое развернутое определение: «Краеведение – всестороннее изучение определенной части страны, города или деревни, друг ...
Вычислить значение функции в точках экстремума
Наибольшее и наименьшее значения функции на отрезке. Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений. Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достига ...
Взаимосвязь обучения и воспитания в творческом поиске педагога
Четыре тезиса постоянно прослеживаются в мировой педагогической литературе ХХ века: обучение – это и есть хорошо организованное воспитание; целью обучения является воспитание гармоничной личности; развивающее обучение – условие и результат воспитывающего обучения; активность личности в обучении осн ...
Педагогика как наука
Обучение было и всегда будет, пока живет человечество. Можно сказать, что подготовка молодого поколения к участию в жизни общества путем передачи социального опыта есть неотъемлемая общественная функция во все времена и у всех народов.
Категории
- Главная
- Методы производственного обучения
- Новые технологии обучения
- Обучение чтению на начальном этапе
- Сущность воспитания
- Информатика и образование
- Формирование деятельности
- Карта сайта