Функция, обратная косинусу

Областью значений функции y=cos x (см. рис. 2) является отрезок. На отрезке функция непрерывна и монотонно убывает.

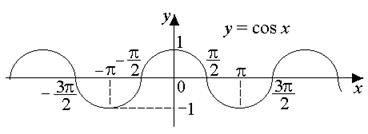
Рис. 2

Значит, на отрезке определена функция, обратная функции y=cos x. Эту обратную функцию называют арккосинусом и обозначают y=arccos x [2].

Определение

Aрккосинусом числа а, если |а|1, называют угол, косинус которого принадлежит отрезку ; его обозначают arccos а.

Таким образом, arccos а есть угол, удовлетворяющий следующим двум условиям: сos (arccos a)=a, |а|1; 0≤ arccos a ≤π.

Например, arccos, так как cos и; arccos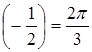, так как cosи .

Функция y = arccos x (рис. 3) определена на отрезке, областью ее значений является отрезок. На отрезке функция y=arccos x непрерывна и монотонно убывает от π до 0 (поскольку y=cos х – непрерывная и монотонно убывающая функция на отрезке ); на концах отрезка она достигает своих экстремальных значений: arccos(–1)= π, arccos 1= 0. Отметим, что arccos 0 = . График функции y = arccos x (см. рис. 3) симметричен графику функции y = cos x относительно прямой y=x .

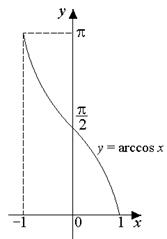
Рис. 3

Покажем, что имеет место равенство arccos(–x) = π–arccos x.

В самом деле, по определению 0 ≤ arcсos х ≤ π. Умножая на (–1) все части последнего двойного неравенства, получаем – π ≤ arcсos х ≤ 0. Прибавляя π ко всем частям последнего неравенства, находим, что 0≤ π–arccos х ≤ π.

Таким образом, значения углов arccos(–х) и π – arccos х принадлежат одному и тому же отрезку. Поскольку на отрезке косинус монотонно убывает, то на нем не может быть двух различных углов, имеющих равные косинусы. Найдем косинусы углов arccos(–х) и π–arccos х. По определению cos (arccos x) = – x, по формулам приведения и по определению имеем: cos (π – – arccos х) = – cos (arccos х)= – х. Итак, косинусы углов равны, значит, равны и сами углы.