Функция, обратная тангенсу
Функция y=tg x на промежутке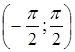 
принимает все числовые значения: E (tg x)=
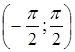. На этом промежутке она непрерывна и монотонно возрастает. Значит, на промежуткеопределена функция, обратная функции y = tg x. Эту обратную функцию называют арктангенсом и обозначают y = arctg x.
Арктангенсом числа а называют угол из промежутка 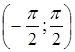, тангенс которого равен а. Таким образом, arctg a есть угол, удовлетворяющий следующим условиям: tg (arctg a) = a и 0 ≤ arctg a ≤ π.
Итак, любому числу х всегда соответствует единственное значение функции y = arctg x (рис. 9).
Очевидно, что D (arctg x) = , E (arctg x) = .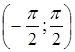
Функция y = arctg x является возрастающей, поскольку функция y = tg x возрастает на промежутке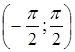. Нетрудно доказать, что arctg(–x) = – arctgx, т.е. что арктангенс – нечетная функция.
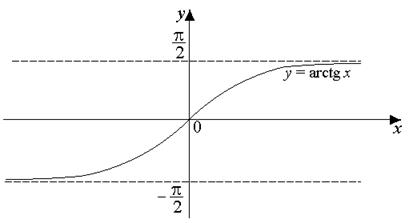
Рис. 9
График функции y = arctg x симметричен графику функции y = tg x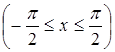 
относительно прямой y = x, график y = arctg x проходит через начало координат (ибо arctg 0 = 0) и симметричен относительно начала координат (как график нечетной функции).
Можно доказать, что arctg (tg x) = x, если x
.
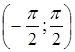Еще по теме:
Развитие словаря в онтогенезе
Развитие словаря тесно связано, с одной стороны, с развитием мышления и других психических процессов, а с другой стороны, с развитием всех компонентов речи, фонетико-фонематического и грамматического строя речи. С помощью речи, слов ребёнок осознает лишь то, что доступно его пониманию. В связи с эт ...
Компьютеры в системе образования
Обучение при помощи компьютера (ОПК) на первых порах основывалось на принципе программированного обучения, где четыре фактора обучения — учитель, ученик, знание и проблема — располагались в непосредственной близости друг от друга. Такой подход осуществляется путем расчленения процесса обучения на л ...
Методика «Дайте название картинке»
В данном практическом параграфе представлении методика «Дай название картинке». Суть данной методики состоит в том, что экспериментатор показывает испытуемым картинки, которые те должны назвать одним словом. Целью данной методики, в частности, является доказательство наличия словотворчества, как за ...
Педагогика как наука
Обучение было и всегда будет, пока живет человечество. Можно сказать, что подготовка молодого поколения к участию в жизни общества путем передачи социального опыта есть неотъемлемая общественная функция во все времена и у всех народов.
Категории
- Главная
- Методы производственного обучения
- Новые технологии обучения
- Обучение чтению на начальном этапе
- Сущность воспитания
- Информатика и образование
- Формирование деятельности
- Карта сайта