Вычислить значение функции в точках экстремума

f(х+2T)=f[(x+T)+T]=f(x+T)=f(x),

f(х+3T)=f[(x+2T)+T]=f(x+2T)=f(x),

f(x)=f[(x-T)+T]=f(x-T)

и т. д. Отсюда, используя метод математической индукции,

Рис. 12

получаем, что для любого п = 0, ±1, ±2, …, выполняется равенство f(х+пТ)=f(х), Таким образом, каждое из чисел nТ (п=1,2,3,…) также является периодом функции f(х).

Мы предполагаем, что читатель хорошо знаком с периодическими функциями sinx, соsx и tgх.

Пример 16. Доказать, что функция является периодической с периодом 2p.

Решение. Область определения рассматриваемой Функции получается выбрасыванием из числовой оси тех точек, в которых знаменатель обращается в нуль, т. е. точек -+2kp (k-целое). Отсюда видно, что если точка х принадлежит области определения рассматриваемой функции f(x), то точки x+2p и x-2p также принадлежат этой области определения. Остается проверить, что выполнено равенство f(x+2p)=f(x). Мы имеем

f(x+2p)=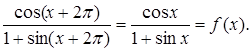

Пример 17. Доказать, что функция f(х)=|sinх| является периодической с периодом p.

Решение. Область определения функции f(х)=|sinх| вся числовая ось. Поэтому для любого k точки х+p и х-p принадлежат области определения. Остается проверить, что выполнено равенство f(х+p)=f(х). Мы имеем f(х+p)=|sin(x+p)|=|-sinx|=|sinx|=f(x).