Вычислить значение функции в точках экстремума

Наибольшее и наименьшее значения функции на отрезке.

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:

Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.

Вычислить значения функции на концах отрезка при x=a, x=b.

Из всех полученных значений выбрать наибольшее и наименьшее.

Приступая к изучению функциональных зависимостей, мы должны, конечно, прежде всего с помощью целесообразной классификации внести хотя бы некоторый порядок в предстоящий нам многообразный мир. Первым таким классифицирующим и организующим принципом служит обычно (и с полным основанием) разделение всех функций на непрерывные и разрывные, причём математический анализ фактически имеет дело почти исключительно с непрерывными функциями, лишь в сравнительно редких случаях привлекая к рассмотрению и простейшие из разрывных. Непрерывные функции обладают целым рядом особых свойств, которых лишены, вообще говоря, функции разрывные; благодаря этим свойствам исследование и применение непрерывных функций весьма значительно облегчаются, так что изучение этих свойств становится для анализа чрезвычайно важным делом.

Мы говорим, что функция у=f(х) непрерывна при х=а (или, короче, в точке а), если f(х)=f(а), или, что в силу определения понятия предела равносильно тому же, если для любой окрестности V числа f(а) найдётся такая окрестность U числа а, что для любого хÎU мы имеем f(х)ÎV. Таким образом, для непрерывности функции в точке а требуется, во-первых, существование предела f(х) и, во-вторых, совпадение этого предела с тем значением, которое функция принимает при х=а. Само собой разумеется, что второе из первого ещё не вытекает, как показывает пример функции

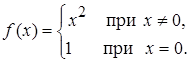(3)

По поводу этого определения надо прежде всего заметить, что так понимаемая непрерывность есть локальное (местное) свойство функции, т. е. такое свойство, которым функция может обладать в одной точке и не обладать в другой; так, функция (3) разрывна (т. е. не непрерывна) при х=0 и непрерывна при любом другом значении х; это - очень важное обстоятельство, которое никогда не надо упускать из вида.

Далее, мы называем, функцию непрерывной в данном отрезке [а,b], если она в вышеприведённом смысле непрерывна в каждой точке этого отрезка; при этом в точке а требуется лишь непрерывность справа, т, е. соотношение f(х)=f(а), а в точке b - непрерывность слева, определяемая аналогичным соотношением, которое Вы напишете сами (если имеется в виду открытый отрезок (а, b), то, разумеется, в точках а и b от функции ничего не требуется). Заметим кстати, что математики давно уже пользуются очень удобным обозначением

f(a)=f(a+0), ,

с помощью которого определение непрерывности функции f(x) в точке а можно записать посредством весьма простого соотношения

f(a+0)=f(a-0)=f(a);

это обозначение не может привести ни к каким смешениям, если только помнить, что f(а+0) и f(а-0) представляют собой не значения функции f(х) в каких-либо точках, а пределы таких значений при некоторых определённых изменениях величины х.

п.1.4.6. периодичность

Функция у=f(х) называется периодической, если существует такое число Т>0, что для, каждого значения х из области определения этой функции значения х+Т и х-Т также принадлежат области определения и выполняется равенство f(x+Т)=f(x). При этом число Т называется периодом функции y=f(x). Из этого определения следует, что