Методика изучения темы "Неравенства" в начальной школе

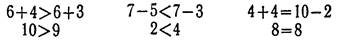
При изучении действий в других концентрах упражнения на сравнение выражений усложняются: более сложными становятся выражения, учащимся предлагаются задания вставить в одно из выражений подходящее число так, чтобы получить верные равенства или неравенства; проверить, верные ли равенства (неравенства) даны, неверные исправить, изменив знак отношения или число в одном из выражений; составить из данных выражений верные равенства или верные неравенства. Сами выражения подбираются таким образом, чтобы, сравнивая выражения, учащиеся наблюдали свойства и зависимости между компонентами и результатами действий. Например, после того как установили с помощью вычислений, что сумма 60+40 больше суммы 60+30, учитель предлагает сравнивать соответствующие слагаемые этих сумм, и дети отмечают, что первые слагаемые в этих суммах одинаковые, а второе слагаемое в первой сумме больше, чем во второй. Много раз, подмечая эту зависимость, учащиеся приходят к обобщению и затем свои знания используют при сравнении выражений.

Таким образом, при изучении всех концентров упражнения на сравнение чисел и выражений, с одной стороны, способствуют формированию понятий о равенствах я неравенствах, а с другой стороны, усвоению знаний о нумерация и арифметических действиях, а также выработке вычислительных навыков.

Неравенства с переменной вида: х+3<7, 10-х>5, х-4>12, 72: х<36 вводятся во II классе. Заранее ведется соответствующая подготовительная работа: включаются упражнения, в которых переменная обозначается не буквой, а "окошечком" (квадратом), например: □ >0, 6+4> □, 7+ □ <10 и т.д. Учащимся предлагается подобрать такое число, чтобы получить верную запись. При выполнении таких упражнений учитель должен побуждать детей к подстановке различных чисел; например, в неравенстве □ >0 можно подставить число 1 (1>□), можно 2 (2>□), можно З (3>□) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).

Рассматривая во II классе, например, неравенство х+3<10, учащиеся путем подбора находят, при каких значениях буквы х значение суммы х+3 меньше, чем 10. В каждом таком задании дается множество чисел - значений переменной. Ученики подставляют значения буквы в выражение, вычисляют значение выражения и сравнивают его с заданным числом. В результате такой работы выбирают значения переменной, при которых данное неравенство является верным.

Термины "решить неравенство", "решение неравенства" не вводятся в начальных классах, поскольку во многих случаях ограничиваются подбором только нескольких значений переменной, при которых получается верное неравенство.

Позднее в упражнениях с неравенствами значения переменной не даются, учащиеся сами подбирают их. Такие упражнения, как правило, выполняются под руководством учителя.

Можно ознакомить детей с таким приемом подбора значений переменной в неравенстве. Пусть дано неравенство 7×k<70. Сначала устанавливают, при каком значении k данное произведение равно 70 (при k=10). Чтобы произведение было меньше, чем 70, следует множитель брать меньше, чем 10. Учащиеся выполняют подстановку чисел 9, 8 и т.д. до нуля, вычисляют и сравнивают полученные значения выражения с заданным (70) и называют ответ.