Функция, обратная котангенсу

Функция y = ctg x на промежутке принимает все числовые значения из промежутка. Область ее значений совпадает с множеством всех действительных чисел. В промежутке функция y = ctg x непрерывна и монотонно возрастает. Значит, на этом промежутке определена функция, обратная функции y = ctg x. Функцию, обратную котангенсу, называют арккотангенсом и обозначают y = arcctg x.

Арккотангенсом числа а называют угол, принадлежащий промежутку, котангенс которого равен а.

Таким образом, аrcctg a есть угол, удовлетворяющий следующим условиям: ctg (arcctg a)=a и 0 ≤ arcctg a ≤ π.

Из определения обратной функции и определения арктангенса следует, что D (arcctg x) = , E (arcctg x) = . Арккотангенс является убывающей функцией, поскольку функция y = ctg x убывает в промежутке.

График функции y = arcctg x не пересекает ось Ох, так как y > 0 R. При х = 0 y = arcctg 0 =[4].

График функции y = arcctg x изображен на рисунке 11.

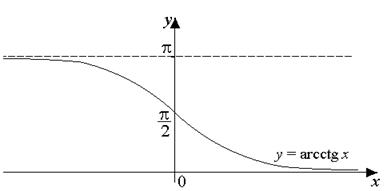
Рис. 11

Отметим, что для всех действительных значений х верно тождество: arcctg(–x) = π–arcctg x.