Графики произведения и частного двух функций

Произведение и частное двух функций поддаются общему исследованию, на основании которого и может быть построен график.

Часто построение графика упрощается, если предварительно построить вспомогательные графики функций, входящих в произведение или частное.

Иногда произведение или частное возможно преобразовать так, что построение графика преобразованной функции оказывается проще.

Эти и некоторые другие приемы построения графиков произведения и частного двух функций иллюстрируются следующими примерами.

y=xsinx (Рис. 53).

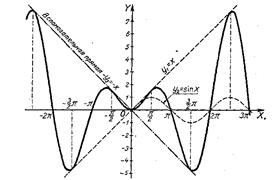
Рис. 53.

Строятся (штриховыми линиями) вспомогательные графики функций, входящих в заданное произведение: у1=х; y2=sinx.

Перемножение этих графиков упрощается благодаря тому, что функция y2=sinx периодически принимает значения 0 и 1. В первом случае искомый график y=xsinx пересекает ось абсцисс, во втором - касается вспомогательной прямой у1=х.

Так как функция y2=sinx периодически принимает еще значение (-1), то построение облегчается, если построить еще одну вспомогательную прямую: у3=-х (на рисунке эта прямая построена штрих-пунктирной линией).

Для всех х=2 заданный график касается этой вспомогательной прямой, так как для этих значений х

sinx=-1.

Так как заданная функция y=xsinx четная [(-x)sin(-х)= =(-х)(-sinx)=xsinx], то указанное построение проводится только для правой части графика; левая часть графика строится затем симметрично правой.

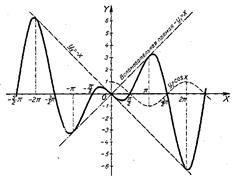
Рис. 54.

2. у= -хcosx (Рис. 54).

Так же, как и в предыдущем случае, помимо графиков двух вспомогательных функций: у1=-х и y2=cosx, входящих в заданное произведение, построен еще третий вспомогательный график функции: у3=х.

Далее построение аналогично предыдущему.

3. y= (Рис. 55).

Замечаем, что заданная функция нечетная, так как == =-. Поэтому построение проводится только для правой части графика, левая часть графика строится затем косо симметрично правой.

На чертеже построены два графика вспомогательных функций, входящих в. заданное частное: и y2=sinx, и третий вспомогательный график: у3=-.

Остальные построения аналогичны предыдущим.

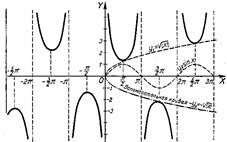
Рис. 55.

Следует особо объяснить вид графика при х®0, так как в этом случае получается неопределенность вида , которую следует раскрыть.

Известно, что , т. е. что при x®0sinx~х. Следовательно, можно записать: