Графики произведения и частного двух функций

4. (Рис. 56).

Функция четная, так как .

Вспомогательные функции: y1=sinx; у2= и y3=

Заданный график строится как график произведения: у1y2=sinx.

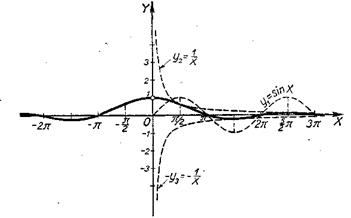
Рис. 56.

y=axlogbx, где а>0; а≠1 и b>1 (Рис. 57).

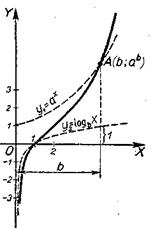Вспомогательные функции: у1=ах; y2=logb x.

Так как область существования функции у2=logb x есть интервал (0, ¥), что определяет область существования заданной функции, то и график вспомогательной функции y1=ах построен только для х>0.

Рис. 57

Заметим, что при x=b y2=logbb=l и у=у1у2=аb, получаем точку А(b;аb).

6. у=|х| (рис. 58).

Функция четная. Построение проводится для правой части графика; левая часть графика симметрична правой.

Вспомогательные графики: у1 =|х|; у2=.

При x=± у2==1, поэтому график заданной функции пересекает прямую y1=|х| в точке A(, ).

При х=±1 у2=0 и у=0.

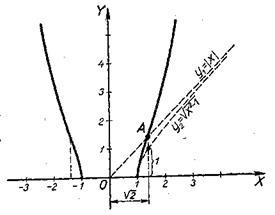
Рис. 58.

7. (Рис. 59).

Функция нечетная, так как

Вспомогательные графики функций y1=arctgх и у2=|х| пoстроены только для х>0.

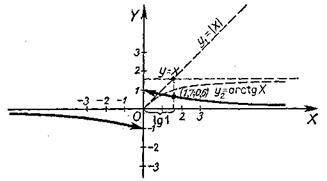
Рис. 59.

Характерные точки (для правой части графика):

1)

так как при х®0 tgx»x;

2);

3) при х= y=; точка (1,7; 0,6).

8. у= (Рис. 60).

Вспомогательные графики: у1=соsх; y2=log4x. Находим область существования заданной функции.

Числитель у1=соsх не дает никаких ограничений для х.

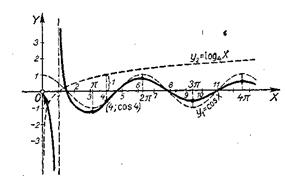
Рис. 60.

Знаменатель y2=log4x обусловливает:

а) х>0,

б) log4x≠0, т. е. х≠1.