Методика изучения основных классов неравенств и их систем

Специфика трансцендентных неравенств. При рассмотрении различных классов трансцендентных неравенств необходимо уделять достаточное внимание формированию навыка применения тождеств для преобразования данных неравенств. Особенно ярко это проявляется в тригонометрии, поэтому при изучении тригонометрических неравенств большое значение приобретают задания и системы вопросов, связанные с распознаванием применимости того или иного тождества, возможности приведения уравнения или неравенства к определенному виду.

Здесь значительные трудности связаны с тем, что некоторые тождества, используемые в преобразованиях, приводят к изменению области определения. К числу таких тождеств относятся, например, такие:

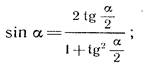
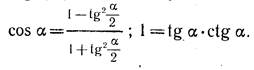
Использование этих тождеств слева направо может привести к потере корней, а справа налево - к появлению посторонних корней. Рассмотрим примеры.

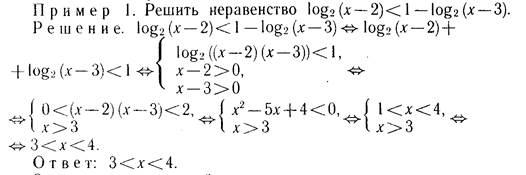
Здесь учет ограничений при использовании тождества для логарифма произведения выполнен при втором переходе, в результате чего неравенство преобразовалось в систему неравенств, из которых два последних позволяют сохранить исходную область определения неизменной.

В результате выполнения аналогичных заданий можно сделать вывод: если приходится пользоваться преобразованиями, расширяющими область определения, то для сохранения равносильности необходимо дополнительно ввести ограничения, сохраняющие исходную область определения неизменной.

В данной работе мы рассмотрели методику преподавания темы "Неравенства" в начальных и старших классах средней школы.

Неравенство числовое - высказывание вида а < b или а > b, где < - отношение строгого порядка, а отношение ≤ - отношение нестрогого порядка на некотором множестве чисел.

Неравенство с переменной - высказывательная форма вида А≤ В, где А или В - высказывательная форма.

Множество значений переменной х (или нескольких переменных), при которых высказывательная форма А < В или А ≤ В истинна, называется множеством истинности этой формы или решением неравенства с переменной.

Иногда неравенство с переменной определяют менее формально, но более, может быть, доступно: два выражения, соединенные знаком неравенства ( - знаки неравенства).

Неравенство, содержащее знак > или <, называют строгим; содержащее знак ≤ или ≥, называют нестрогим. Отношения "меньше" и "больше" для чисел а и b взаимосвязаны: если а>b, то b<а; если а<b, то b>а.

К обеим частям истинного (верного) числового неравенства можно прибавлять одно и то же число, в результате получим истинное неравенство. Умножая обе части истинного числового неравенства а<b на положительное число с, получим истинное неравенство ас<bс; если умножить на одно и то же отрицательное число с и изменить знак неравенства на противоположный, то получится истинное неравенство ас>bс.