Общетеоретические основы темы «Обратные тригонометрические функции»

Функции arcsin x, arccos x и т.д. обратны функциям sin x, cos x и т.д. (подобно тому как функция обратна функции , поэтому они называются обратными тригонометрическими функциями (иначе круговыми). Все обратные тригонометрические функции многозначны, т.е. для каждой из них справедливо следующее: одному значению x соответствует множество (бесчисленное) значений функции (так как бесчисленно множество углов, например α, 180° – α, 360°+ α имеют один и тот же синус).

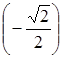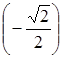Главным значением arcsin x называется то его значение, которое заключено между – π/2 (–90°) и π/2 (+ 90°). Так, главное значение arcsin есть, главное значение arcsin есть . Главным значением arccos x называется то его значение, которое заключено между 0 и π (+180°). Так, главное значение arccos есть, главное значение arccos есть .

Главные значения arctg x и arcsec x (как и arccos x) cодержатся между 0 и π. Главные значения arctg x и arcsec x (так же как и arcsin x) находятся между –π/2 и π/2.

Главные значения: arctg (–1) = –π/4, arсctg = π/6, arcsec (–2)= 2π/3.

Если через Arcsin x, Arccos x и т.д. обозначим любое из значений соответствующих обратных тригонометрических функций, а для главных значений сохранить обозначения arcsin x, arccos x и т.д., то связь между значениями обратной тригонометрической функции и ее главным значением представится следующими формулами:

Arcsin x = kπ+(-1)k arcsin x,

Arccos x=2kπarccos x,

Arctg x= kπ+ arctg x,

Arcctg x= kπ+arcctg x,

где k – любое целое число (положительное, отрицательное или нуль).