Задачи по геометрии, решаемые методами оригами

Можно ли двумя разрезами разбить треугольник на восемь треугольников?

Какое количество треугольников можно получить при проведении трех разрезов данного треугольника?

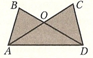
Сколько треугольников изображено на рисунке? Назовите их.

Сколько углов вы видите на рисунке? Назовите их.

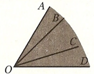
Сосчитайте сколько треугольников изображено на рисунке?

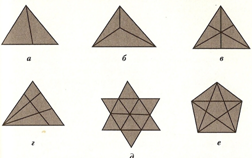
Схема рассуждений

Цепочка задач построена таким образом, что при переходе к каждой последующей фигуре увеличивается число искомых треугольников (принцип нарушается при переходе от случая «в» к случаю «г», но в случае «г» усложняется «геометрический фон», т.е. появляются такие взаимопроникающие треугольники, которые состоят, например, из треугольника и четырехугольника, а в случае «в» все взаимопроникающие треугольники можно рассматривать состоящими только из треугольников).

Оценка выполнения задания

Случай «а»

Если учащийся увидел большой треугольник, состоящий из двух маленьких, т.е. всего три треугольника, то он получает 1 балл.

Если учащийся не видит какой-либо из трех треугольников, то он получает 0 баллов.

Случай «б»

На данном рисунке изображен большой треугольник, состоящий из трех маленьких, всего четыре треугольника. Такое решение оценивается в 1 балл.

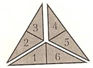
Случай «в»

Схема рассуждений и ход решения

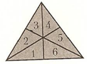
Сосчитаем все маленькие треугольники, их всего шесть

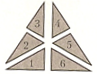
Сосчитаем треугольники, состоящие из двух маленьких, их всего три

Сосчитаем треугольники, состоящие из трех маленьких, их всего шесть

Треугольник, состоящий из шести маленьких треугольников – 2

Всего получилось 16 треугольников

Оценка выполнения задания

Учащиеся сосчитали (увидели) все взаимопроникающие треугольники, подсчет вели с помощью алгоритма – 2 балла.

Задача решалась без применения алгоритма (какие треугольники учащийся увидел, такие и сосчитал, но нашел больше семи треугольников – 1 балл).

Учащийся при решении насчитал меньше семи треугольников, т.е. не увидел взаимопроникающих треугольников, - оценка 0 баллов.

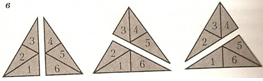
Случай «г»

Схема рассуждений и ход решения

Сосчитаем треугольники в «нижней» части рисунка, их всего шесть, причем все они состоят только из треугольников.

Добавляем «верхнюю» часть, получаем треугольники, состоящие из треугольников и четырехугольника.

Всего получилось: (3+2+1)+(3+2+1)=12 треугольников.

Оценка выполнения задания

Учащийся подсчитал все треугольники с помощью алгоритма (выбор алгоритма значения не имеет) – оценка 3 балла.

Учащийся применил для решения алгоритм, не позволяющий выделить все имеющиеся на рисунке треугольники – оценка 2 балла.

Учащиеся, не увидевшие взаимопроникающих треугольников, получают 1 балл.

Учащиеся, увидевшие на рисунке меньше семи треугольников, получают 0 баллов.

Сосчитайте число треугольников, изображенных на рисунке.

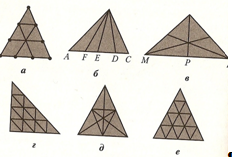
Ответы: а) 13 треугольников; б) 27 треугольников; в) 47 треугольников; г) 27 треугольников; д) 32 треугольника; е) 48 треугольников.

Начертите треугольник. Пересеките его двумя прямыми так, чтобы на рисунке оказалось:

а) Пять треугольников

Схема рассуждений

Надо получить пять треугольников. Один треугольник уже есть, он построен по условию задачи. Если из любой вершины провести прямую, пересекающую противоположную сторону, то получим еще два треугольника. В одном из полученных треугольников через вершину, лежащую на стороне исходного треугольника, проведем прямую, пересекающую противоположную сторону этого треугольника, получим еще два треугольника.

б) Восемь треугольников

Схема рассуждений

Чтобы получилось семь треугольников (один уже есть), достаточно провести прямые через две вершины, пересекающие противоположные им стороны исходного треугольника.

Оценка выполнения задания

Верное решение оценивается в 3 балла. Попытки, близкие к верному решению, - 1 балл и неверно решенная задача – 0 баллов.

"Цепочки" задач по теме "Точки и прямые плоскости"

Задачи направлены на развитие математических способностей учащихся.

В этом разделе содержатся задачи, которые интересны и полезны для учащихся любого возраста.