Задачи по геометрии, решаемые методами оригами

Постройте два угла, стороны которых попарно параллельны, таким образом, чтобы при пересечении этих сторон образовался прямоугольник, имеющий площадь 6 дм2.

Постройте два угла, стороны которых попарно перпендикулярны, таким образом, чтобы при пересечении этих сторон образовался отрезок, имеющий длину 2 дм.

Треугольники

Постройте треугольник, у которого длина первой стороны больше 2 дм, но меньше 3 дм, длина второй стороны больше 3 дм, но меньше 4 дм, длина третьей стороны больше 4 дм, но меньше 5 дм.

Четырех угольники

Постройте четырехугольник, все стороны которого имеют длину, равную диагонали прямоугольника размером 3х1 дм. Найдите несколько решений.

Постройте четырехугольник, все стороны которого имеют различные длины от 4 до 5 дм.

Постройте квадрат со стороной 6 дм. Постройте все различные квадраты, вершины которых лежат на сторонах исходного квадрата.

Постройте прямоугольник, площадь которого равна 12 дм2, четырьмя различными способами.

Постройте шесть квадратов, площади которых равны 4 дм2, 16 дм2, 64 дм2, таким образом, чтобы каждый меньший по площади квадрат содержался внутри каждого большего.

Постройте два прямоугольника, имеющих: а)равные периметры и равные площади; б)равные площади и разные периметры.

Геометрия на клетчатой бумаге

Рекомендации по проведению уроков

Начинать обучать школьников желательно с пятого класса.

Преподавание должно вестись непринужденно, почти в импровизационном стиле. Эта видимая легкость на самом деле требует от учителя большой и серьезной подготовки.

Занятия лучше проводить в нестандартной форме.

Необходимо использовать на уроках как можно больше наглядного материала: различных карточек, картинок, наборов фигур, иллюстраций к решению задач, схем.

При разборе темы нужно стараться добиваться понимания, а не зазубривания.

Урок №1

Цель: развивать комбинаторные навыки (рассмотреть различные способы построения линии разреза фигур, правила, позволяющие при построении этой линии не терять решения), развивать представления о симметрии.

Задачи 1-4 решаем на уроке, задача 5 – на дом.

Квадрат содержит 16 клеток. Разделите квадрат не две равные части так, чтобы линия разреза шла по сторонам клеток. (Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, не равны частям, полученным при другом способе). Сколько всего разрезаний имеет задача?

Указание. Найти несколько решений этой задачи не так уж сложно. На рисунке некоторые из них показаны, причем решения б) и в) одинаковы, так полученные в них фигур можно совместить наложением (если повернуть квадрат в) на 90 градусов).

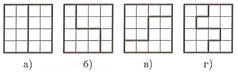
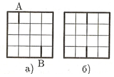
Но найти все решения и ни одно решение не потерять уже труднее. Заметим, что ломаная, делящая квадрат на две равные части симметрична относительно центра квадрата. Это наблюдение позволяет шаг за шагом рисовать ломаную с двух концов. Например, если начало ломаной в точке А, то конец ее будет в точке В. Убедитесь, что для данной задачи начало и конец ломаной можно нарисовать двумя способами.

При построении ломаной, чтобы не потерять какое-либо решение, можно придерживаться такого правила. Если следующее звено ломаной можно нарисовать двумя способами, то сначала нужно заготовить второй такой же рисунок и выполнить этот шаг на одном рисунке первым, а на другом вторым способом. Аналогично нужно поступать, когда способов не два, а три. Указанный порядок действий помогает найти все решения.

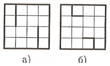
Прямоугольник 3х4 содержит 12 клеток. Найдите пять способов разрезания прямоугольника на две равные части так, чтобы линия разреза шла по сторонам клеток (способы разрезания считаются различными, если части, полученные при одном способе разрезания, не равны частям, полученным при другом способе).

Прямоугольник 3х5 содержит 15 клеток и центральная клетка удалена. Найдите пять способов разрезания оставшейся фигуры на две равные части так, чтобы линия разреза шла по сторонам клеток.

Квадрат 6х6 разграфлен на 36 одинаковых квадратов. Найдите пять способов разрезания квадрата на две равные части так, чтобы линия разреза шла по сторонам квадрата.

Задача 4 имеет более 200 решений. Найдите хотя бы 5 из них.

Урок №2

Цель: продолжать развивать представления о симметрии (осевой, центральной).

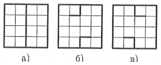
Разрежьте фигуры, изображенные на рисунке, на две равные части по линиям сетки, причем в каждой из частей должен быть кружок.