Задачи по геометрии, решаемые методами оригами

В предлагаемых задачах прекрасно работает "математическая интуиция" и "математическое воображение", которые в среднем школьном возрасте как бы полностью открыты, ничем не загромождены (знания и опыт часто заслоняют эти очень важные качества). Интуитивное предвидение верных фактов, комбинаций и даже методов – это одно из огромных достоинств предлагаемых ниже задач.

Сначала рассмотрим задачи, для решения которых фактически не требуется никаких теоретических знаний.

Методические рекомендации: данные задачи можно использовать для устной работы при проведении урока на этапе актуализации знаний.

Есть одна точка. Проведите через эту точку прямую. Сколько прямых можно провести через данную точку? Какая фигура при этом получится плоская или пространственная?

Есть три точки. Как они могут быть расположены? Сколько через них можно провести прямых? Почему? (Эта задача может быть сформулирована для любого числа точек).

На листе бумаги отметили пять точек и провели всевозможные прямые, каждая из которых проходит через какие-либо две из этих точек. Как расположить точки, чтобы оказались проведенными: а) пять прямых; б) шесть прямых?

На листе бумаги отметили n точек и провели всевозможные прямые, каждая из которых проходит через какие-либо из этих точек. Оказалось, что проведено шесть прямых. Возможно ли, что n=3; n=4; n=5; n=6? Для тех случаев, когда это возможно, сделайте чертежи.

На полу классной комнаты отметим мелом точу А.

Сколько прямых задают эта точка А и точки, являющиеся вершинами углов в классной комнате? Сделайте чертежи, обозначьте вершины углов класса и выпишите все получившиеся прямые.

Представьте себе, что на каждой стене класса отмечена точка (сколько таких точек отмечено?). Мысленно соедините эти точки прямыми. Сколько образовалось прямых?

Сколько получится прямых, если добавить к точкам на стенах класса точку А, отмеченную на полу классной комнаты?

Ниже приведем систему творческих задач, решение которых требует нестандартного подхода.

Методические рекомендации: задачи из данной группы можно использовать как дополнительный материал на уроке для тех детей, которые раньше всех справятся с заданием на урок. За выполнение этих заданий можно поставить оценку в журнал.

Могут ли шесть прямых пересекаться в восьми точках?

Могут ли семь прямых пересекаться в восьми точках? Сколько точек пересечения может быть у семи прямых?

Как расположить пять точек и две прямые, чтобы на каждой прямой было по три точки?

Можно ли шесть деревьев посадить в четыре ряда так, чтобы в каждом ряду было по три дерева?

Разработка урока по теме "Угол"

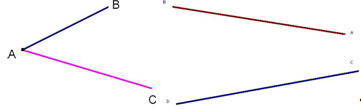
Учащимся предлагается рассмотреть заранее заготовленные рисунки. Перед учащимися ставятся вопросы:

– Назовите лучи, изображенные на рисунках.

– Назовите начало каждого луча.

– Что можно сказать о лучах на рисунке 2? (Они имеют общее начало – точку А).

– Что можно сказать о лучах на рисунке 1? (Начало лучей в разных точках).

– Показать область плоскости, на которые ее делят лучи на рисунке 2.

– Можно ли указать определенные части плоскости, на которые ее делят лучи на рисунке1? (Нет).

По "рис.3" предлагаются вопросы:

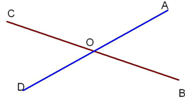
– Назовите лучи, имеющие общее начало и лежащие в одной области плоскости. (ОА и ОВ, ОА и ОС, ОС и ОD, ОD и ОВ)

– Назовите пары лучей, имеющие общее начало. (ОА и ОВ, ОА и ОС, ОС и ОD, ОD и ОВ, ОD и ОА, ОВ и ОС)

– Покажите области, на которые делят ее пары лучей.

3. После такой подготовительной работы дается понятие угла. По рис. 1, 2 предлагается указать угол, выясняется, каких признаков угла недостает на рис.1.

4. Вводится обозначение угла по рис.2 (А – вершина, АВ и АС – стороны, чтение угла).

5. Под руководством учителя всеми учащимися проводится практическая работа: “Из листа бумаги вырезать угол”. Учащиеся приготавливают лист бумаги, чертежные инструменты, ножницы. Выясняется последовательность построения угла, выбирается начало (вершина), проводятся два произвольных луча из вершины. Учащиеся строят угол. Вырезают. Учитель, выполняя у всех на глазах эту же работу, предлагает задание учащимся:

– Покажите угол.

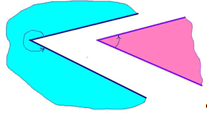
– Что представляет собой оставшаяся часть? (Выясняется, что тоже угол – обе фигуры часто называют плоским углом.)

Делается вывод: получили две фигуры, каждая есть угол. Учащимся указывается обозначение угла.

6. Предлагается начертить в тетради произвольный угол, назвать его, сделать подпись под чертежом. (Эту же работу выполняет ученик, вызванный к доске). После выполнения задания учащиеся сверяют его с чертежом на доске. Еще раз в памяти детей восстанавливается понятие угла, его обозначение, чтение.