Задачи по геометрии, решаемые методами оригами

Слово "оригами" происходит от двух японских слов: "ори" – сложенный, "ками" – бумага, и может быть переведено как "сложенная бумага". Складывание фигурок из бумаги имеет многовековую историю и своими корнями тесно связано с культурой Востока.

Неопределяемыми понятиями геометрии являются: точка, прямая и плоскость. В традиционном школьном курсе геометрии решаются задачи на построение при помощи циркуля и линейки. В решении таких задач с помощью линейки можно провести произвольную прямую; произвольную прямую, проходящую через данную точку; прямую, проходящую через две данные точки. При помощи циркуля можно описать окружность данного радиуса и отложить отрезок на данной прямой от данной точки.

Возможности перегибания листа бумаги включают в себя не только "геометрию линейки", но и "геометрию циркуля", что обеспечивает возможность решения большого разнообразия серьезных, а порой и забавных задач. Как правило, решение задач методами перегибаний (оригами) проще и нагляднее. Некоторые задачи, решаемые методами оригами, при помощи циркуля и линейки просто не имеют решения!

Наглядность и относительная простота освоения оригами могут помочь и при изучении геометрии. Такой подход оживляет и заметно облегчает освоение целого ряда абстрактных, и потому сложных для освоения многим учащимся геометрических понятий, делает их изучение более ясным и доступным, убеждает в правильности классических утверждений, теорем и побуждает к дальнейшим исследованиям. Ученики учатся понимать то, о чем говорят сами, и то, что говорят другие, учатся мыслить.

Условные знаки и приемы складывания

Деление отрезка на равные части

Из произвольного листа бумаги при помощи сгибов можно получить квадрат. Если на этом листе бумаги дан отрезок, который требуется разделить, то всегда сначала можно построить квадрат со стороной равной этому отрезку, а затем разделить сторону квадрата.

В задачах этого раздела происходит деление на равные части стороны квадрата (прямоугольника) при этом подразумевается, что длина заданного отрезка равна стороне квадрата.

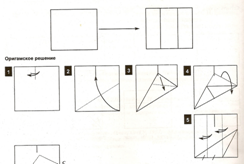
Методом перегибания точно разделить сторону квадрата на три равные части.

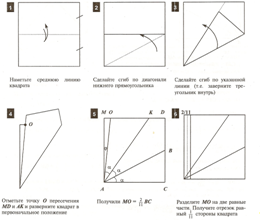
Разделить сторону квадрата на 11 равных частей

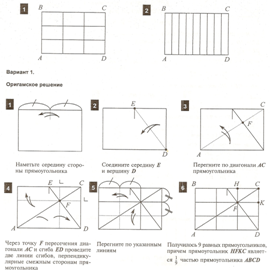
Разделить прямоугольник ABCD на 9 равных прямоугольников, не используя измерительных приборов, как на рисунках 1 и 2.

Вариант 2

Прямой угол

Методом складывания разделить один из углов квадрата на три равных угла

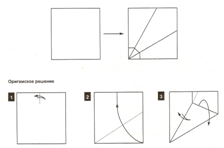
Геометрия листа произвольной формы

Из произвольного листа бумаги получите с помощью сгибов квадрат

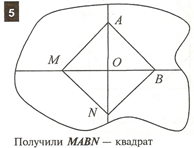
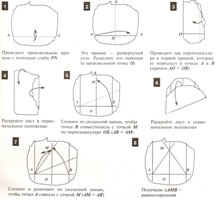
Из произвольного листа бумаги получить равносторонний треугольник

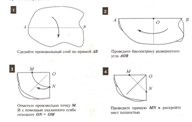
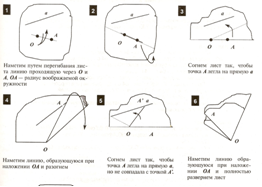
На листе бумаги проведены прямая, а также даны центр окружности и некоторая точка на ней (сама окружность не нарисована). Как с помощью перегибаний найти точки пересечения воображаемой окружности с проведенной прямой?

О- центр окружности

А- лежит на окружности

Задачи на геоплане

Что такое геоплан?

Геоплан представляет собой плоскую поверхность с закрепленными на ней тонкими стержнями, располагающимися в форме квадратной сетки или каким-либо другим способом (в виде окружности, многоугольника). Построение фигур осуществляется на геоплане при помощи эластичных шнуров (резиновых нитей или колец), которые фиксируются между стержнями.

Главное достоинство геоплана состоит в возможности быстрого построения геометрических фигур. При этом не требуются ни бумага с карандашом, ни доска с мелом и не нужно ничего стирать: любую конфигурацию можно быстро изменить или построить заново.

Как строить фигуры на геоплане

Строить (изображать) на геоплане можно различные геометрические фигуры: отрезки, углы, ломаные, треугольники, квадраты, ромбы, прямоугольники, параллелограммы, трапеции, всевозможные многоугольники, а также различные конфигурации, образованные линиями. Можно иллюстрировать или устанавливать свойства геометрический фигур: равенство сторон, углов, площадей, периметров.