Различные современные подходы к определению понятия «функция»

Заметим, что в примерах 4 и 5 одинакова область значений D и одинаково правило соответствия: формулы a1+(n-1)r и а1+(х-1)r показывают, что в обоих случаях надо над выбранным числом (n или х) проделать одни и те же действия, чтобы узнать, какое число поставлено ему в соответствие. Однако области определения этих двух функций различны, и потому мы имеем в примерах 4 и 5 разные функции. Таким образом, для задания функции мало указать правило соответствия, а надо еще обязательно указать область определения и область значений.

Для обозначения функций обычно пользуются буквами. Одна буква (чаще всего х) используется для обозначения произвольного элемента, взятого из области определения функции. Эта буква называется аргументом. Таким образом, если сказано, что х - аргумент некоторой функции, то вместо х мы можем подставить любой элемент, принадлежащий области определения этой функции. Далее, другая буква (чаще всего у) используется для обозначения произвольного элемента, взятого из области значений. Эта буква называется функцией (и это второе значение слова «функция»). Наконец, третья буква (чаще всего f) используется для обозначения правила соответствия. Это значит, что если а - произвольное значение аргумента (т. е. произвольный элемент, взятый из области определения функции), то элемент, поставленный ему в соответствие, обозначается через f(а). Элемент y = f(а) называется значением рассматриваемой функции при х=а.

Все три буквы х, у, f объединяются одной записью:

y=f(x) (1)

(«игрек равен эф от икс»), которая и означает, что х - аргумент, у - функция, а f - правило соответствия. Иногда букву f или выражение f(х) также называют функцией (и это - уже третье значение слова «функция»).

Пример 6. Обратимся снова к функции, рассмотренной в примере 4. Аргумент обозначим через п, функцию - через у, а правило соответствия - через f. Таким образом, мы запишем эту функцию в виде у=f(n). Вот несколько значений этой функции:

f(1)=a1, f(2)=a2=a1+r, f(3)=a3=a1+2r и т. д.

Разумеется, вместо букв х, у, f можно использовать и другие буквы. Например, запись s=j(t) означает, что s есть функция аргумента t (или короче: s есть функция от t), причем правило соответствия обозначается буквой j.

Следует подчеркнуть, что область значений функции представляет собой множество элементов (или чисел), среди которых обязательно содержатся все значения рассматриваемой функции. Однако в области значений могут содержаться и «лишние» элементы, не являющиеся значениями функции. Иными словами, множество значений функции обязательно содержится в области значений, но не обязательно совпадает с ней. Так, в примере 3 значениями функции являются лишь положительные числа, тогда как область значений есть множество всех действительных чисел. Несовпадение множества значений функции и области значений можно видеть также в примере 4.

В заключение рассмотрим еще одно (четвертое!) понимание слово «функция», являющееся для школьного курса математики наиболее важным. Именно, функцией называют произвольное выражение, содержащее аргумент х, а также знаки действий и числа. Например, функциями (в этом смысле) являются

y=x2+1, (2)

y=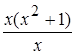, (3)

y=|x-1|, (4)

y=, (5)