Вспомогательные приемы построения усложненных графиков

Известно, что методы высшей математики позволяют строить любой график. Однако знаний тех элементов высшей математики, которые даются в средней школе, для этой цели недостаточно. С другой стороны, большое количество графиков, иногда весьма интересных может быть построено средствами исключительно элементарной математики. Наиболее трудные из этих графиков требуют для своего построения хорошего знания многих разделов элементарной математики, а подчас и остроумного применения этих знаний. Построение графиков средствами элементарной математики может служить материалом для закрепления и усовершенствования учениками и абитуриентами своих знаний по многим важным разделам элементарной математики.

Разобьем этот прием на примере построения графика функции

График этой функции можно построить, пользуясь общими приемами:

область существования: (-¥;¥), т.е. вся числовая ось;

область изменения функции – полуоткрытый интервал 1£у<¥;

функция четная;

при х=0 у=1, т.е. кривая пересекает ось у-ов в точке (0;1); в этой точке функция имеет минимум, так как х2 =0, откуда у³1;

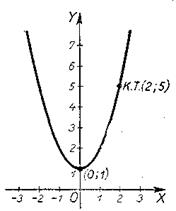
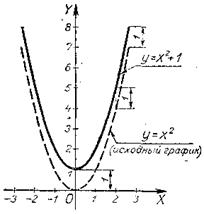
Рис.13. Рис.14.

контрольная точка: при х=2 у=4+1=5; точка (2; 5).

По этим данным график функции построен на рис. 13.

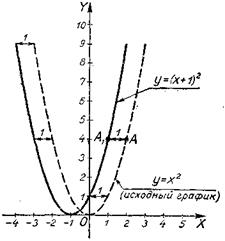
Тот же график можно построить проще, воспользовавшись уже известным нам графиком функции у=х2. Для этого наносим штриховой линией график функции у=х2 (рис. 14), назовем его исходным графиком.

Сравнивая графики функций у=х2+1 и у=х2, видим, что ординаты у графика заданной функции на 1 больше ординат исходного графика. Следовательно, исходный график надо перенести на 1 вверх, как это и сделано на рисунке 14.

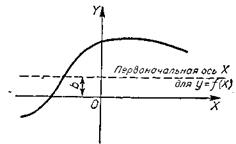
График функции у=х2+1 можно построить еще проще, если воспользоваться тем же исходным графиком (y=x2), но вместо перенесения всей кривой вверх на 1 перенести ось х-ов на ту же 1 вниз, как показано на рисунке 15. Тем самым относительно новой оси х-ов все ординаты

кривой у=х2 увеличиваются на 1 и получается график заданной функции у=х2+1.

Следовательно, график функции y=f(x)+b, где f(x) - простейшая функция, график которой нам известен, можно построить следующим простейшим приемом (рис. 15).

Строится известный нам график функции у=f(х), причем горизонтальная ось вычерчивается штриховой линией. Затем она сдвигается на (-b). Это и есть истинная ось х-ов; первоначальную же горизонтальную ось, нанесенную штриховой линией, можно стереть.

Например, для построения графика функции у=f(x)+3 горизонтальная штриховая ось графика функции у=f(x) сдвигается на 3 единицы вниз, т. е. на (-3); для построения графика функции y=f(x)-3 горизонтальная штриховая ось сдвигается на (+3), т. е. на 3 единицы вверх.

Разберем этот прием на примере построения графика функции

y=(x+1)2.

Общий метод построения графика:

область существования — вся числовая ось;

область изменения функции - полуоткрытый интервал 0£у<¥;

функция не обладает свойствами четности и нечетности;

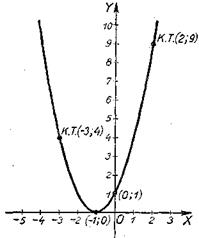
при у=0 (х+1)2=0, или х+1=0, откуда х=-1, т. е. кривая пересекает ось х-ов в точке (-1; 0);

при х=0 у=1, т. е. кривая пересекает ось у-ов в точке (0; 1);

контрольные точки:

x=2; у=(2+1)2=9; точка (2; 9);

x=-3; у=(-3+1)2=4; точка (-3; 4).

По этим данным график функции построен на рисунке 17.