Вспомогательные приемы построения усложненных графиков

График функции y=sinx можно построить проще, приняв за исходный известный нам график функции y=sinx, нанесенный штриховой

линией на рисунке 24. Замечаем, что период исходной функции y=sinx w0=2p, а период заданной функции y=sinx w=4p,

Рис. 23

т. е. вдвое больше периода исходной функции. Таким образом, график, который требуется построить, получится из исходного графика (штрихового, на рисунке 24) путем растяжения его по оси х-ов вдвое.

Рис. 24

2-й пример (на сжатие).

y=sin3x.

Общий метод построения графика тот же, что и в примере первом:

1-й и 2-й пункты исследования те же;

3) период функции находится из равенства

sin3x=sin(3x+2p)=sin3(x+),

откуда период w=, полупериод ;

4) характерные точки:

а) при у=0 sin3x=0, откуда 3х=, х=, т. е. кривая пересекает ось х-ов в точках (0; 0) и (; 0);

б) максимум функции равен 1 при 3х=, т.е. при х=.

По этим данным график построен на рисунке 25 в той же последовательности, как и предыдущий график.

Рис. 25.

График функции у=sin3x проще построить методом сжатия по ocи x-ов исходного графика y=sinx в 3 раза (рис. 26), так как период ; заданной функции в 3 раза меньше периода 2p исходной функции.

Рис. 26.

Таким образом, график функции y=f(nx), если известен график функции y=f(x), с строится посредством сжатия по оси х-ов этого исходного графика пропорционально коэффициенту п при аргументе, а именно:

если п>1, то сжатие в п раз;

если 0<п<1, то растяжение в раз.

п.3.2.2 По оси у-ов

1-й пример (на растяжение).

у=2sinx.

Строить этот график методом полного исследования функции нецелесообразно. Отчетливо видно, что ординаты графика в 2 раза больше ординат исходного трафика y=sinx. Поэтому график заданной функции строится путем удвоения всех ординат исходного графика, т.е. путем растяжения исходного графика по оси у-ов 2 раза (рис. 27).

2-й пример (на сжатие).

у=sinх.

По тем же соображениям этот график строится способом уменьшения всех ординат исходного графика в 3 раза, т. е. сжатием исходного графика по оси у-ов в 3 раза, что сделано на том же рисунке 27.

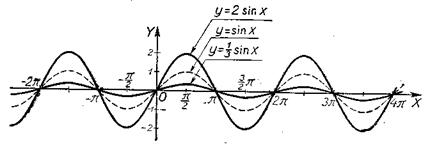
Рис. 86.

Таким образом, график функции y=mf(x), если известен график y=f(x), строится посредством растяжения по оси у-ов исходного графика пропорционально коэффициенту т при функции, а именно:

если т>1, то растяжение в т раз;

если 0<т<1, то сжатие в раз.

Примечание 1. Если требуется построить график функции y=mf(nx), то сначала строится штриховой линией график исходной функции у=f(х), а затем этот исходный график сжимается по оси х-ов в п раз и растягивается по оси у-ов в т раз.

Примечание 2. На графиках, разобранных в этой главе, все исходные штриховые линии (первоначальные оси координат, сдвинутые в дальнейшем, и исходные графики) можно стереть или перечеркнуть по окончании всех построений.

График функции y=-f(x) получается зеркальным отражением графика функции y=f(x) относительно оси х (рис. 28)

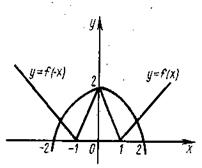
График функции y=f(-x) получается зеркальным отражением графика функции y=f(x) относительно оси у (рис. 29)

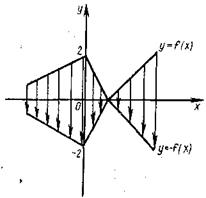
Рис. 28. Рис. 29.

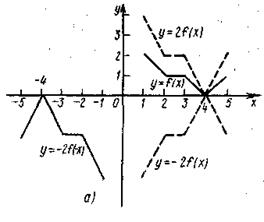1. Построить график функции если дан график функции y=f(x).(рис. 30, а)