График суммы и разности двух функций

Строим два вспомогательных графика:

y1=x и у2=arcsinx.

Ординаты искомого графика представляют собой разность: у1-у2. Характерные точки:

1) х=0, у1=0; у2=0; у=0; точка (0; 0);

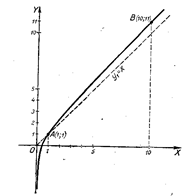
рис. 33

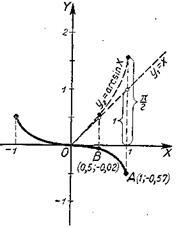2) х=1 (граничная точка), у1=1, y2=arcsin1=, у=-1»-0,57; точка (1;-0,57);

3) х=0,5, у1=0,5, у2=arcsin0,5=»0,52; у=-0,02; точка (0,5;-0,02).

Левая часть графика построена косо симметрично правой.

Из рисунка видно, что область существования заданной функции та же, что для

Рис. 34 второго слагаемого, т. е. для функции y2=arcsinх - сегмент [-1; 1].

5. y=arcctgx-x (рис. 35).

Строим вспомогательные графики:

у1=arcctgх и у2=-х.

Ординаты обоих графиков складываются. Замечаем, что прямая у2=-х является асимптотой заданной кривой. Вторая асимптота

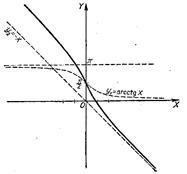
Рис. 35

имеет уравнение: у3=p-х. Характерная точка: при х=0 y=arcctg0=; точка (0; ). Далее, =p+∞=∞.

6. y=sin(arcsinx)-х (рис. 36).

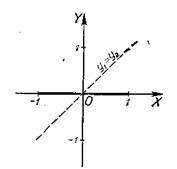
Рис. 36. Рис. 37.

Область существования [-1; 1] заданной функции совпадает с областью существования функции y1=sin(arcsinx). В этой области y1=sin(arcsinx)=x, также и у2=х.

Следовательно, у=у1-у2=0

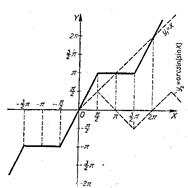
Рис. 38.

График функции - отрезок оси х-ов в пределах [-1; +1].

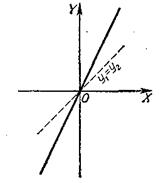
7. y=х-ctg(arcctgх) (рис. 37).

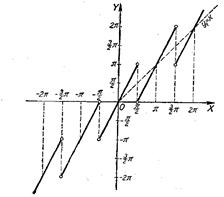
Рис. 39.

Область существования заданной функции — вся числовая ось х-ов (-∞; ∞).

у1=х;

y2=ctg(arcctgх)=х;

у=у1+у2=х+х=2х.

График функции — прямая, проходящая через начало координат под углом a к оси х-ов, где

a=arctg2.

8. y=x+arcsin(sinx) (рис. 38).

Заданная функция нечетная. Поэтому построение графика проводим только для х≥0.

Строим полупрямую у1=х и от нее откладываем соответствующие значения функции у2=arcsin(sinх). Левая часть графика строится косо симметрично правой.

9. y=х+arctg(tgx) (рис. 39).

Построение этого графика аналогично построению предыдущего графика.

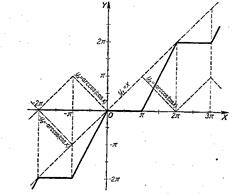
Рис. 40.

10. у=х-arccos(cosх) (рис. 40). Строим два вспомогательных графика:

у1=х и у2=аrссоs(соsx).

Справа от вертикальной оси ординаты графика заданной функции получаются как разность соответствующих ординат вспомогательных графиков: