График суммы и разности двух функций

Так как среднее арифметическое двух положительных чисел больше среднего геометрического этих чисел или ему равно, то

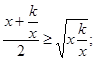
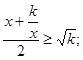
Минимальное значение суммы имеет место при условии, что =2; откуда получаем:

; ;

x= и

Для заданной функции, следовательно, имеем:

при х==.

Левая ветвь графика косо симметрична правой.

20. у=х- (рис. 50).

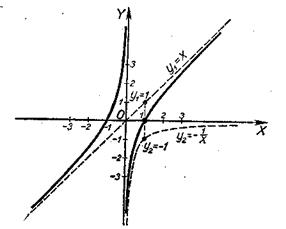
Рис. 50.

Функция нечетная. Построение проведено для х>0.

Вспомогательные функции: у1=х и у2=-.

Ординаты искомого графика получаются алгебраическим сложением ординат у1 и у2. Так как ординаты графика у2 отрицательны, то они откладываются вниз от графика у1.

Прямая у1=х является асимптотой для искомого графика, причем правая ветвь графика приближается к этой асимптоте снизу Кроме того, имеем:

при х®0 у=х-®-∞;

при х=1 у1=1; -у2=-1; у=у1 - у2=0.

21. y=sinx+cosx (рис. 51).

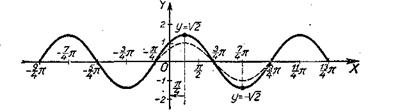
Рис. 51.

Преобразуем заданную функцию:

.

Строим график преобразованной функции:

.

22. y=cosx- sinx (рис. 52)

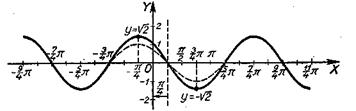
Рис. 52.

Аналогично предыдущему преобразуем данную функцию:

и строим график функции:

.