График суммы и разности двух функций

y=y1-y2.

Слева от оси у-ов сделано дополнительное построение графика функции - у2= - arccos(cos x). Затем ординаты у1 и (- у2) складываются.

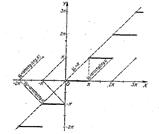
рис. 41.

11. у=х - arcctg (ctg x) (рис. 41).

График этой функции строится так же, как и предыдущий.

12. y=+lgx (рис. 42).

Вспомогательный график у1=. Ординаты функции y2=lgx откладываются не от оси х-ов, а от вспомогательного графика у1. Характерные точки:

1) при x=l y1==l; y2=lgl=0; у=1; точка А(1; 1);

2) при х=10 у1=; y2=lgl0=l; y=+l; точка В(10; +1);

3) =-∞.

Область существования заданной функции: (0; ∞), т.е. та же, что и функции y2=lgx.

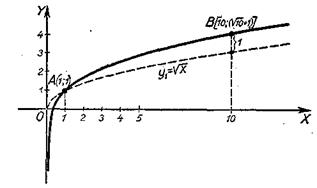
Рис. 42.

13. у=- cos x (рис. 43).

Строим графики двух функций (штриховыми линиями): у1= и у2=-соsх. Второй график построен только для х≥0, т.е. в пределах области существования функции у1=. График заданной функции строится в этих же пределах сложением ординат: y1+у2.

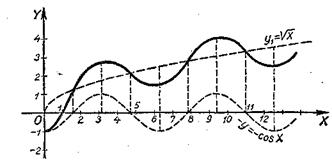
рис. 43.

14. y=arcsin(sinx)- (рис. 44).

Помимо двух вспомогательных графиков функций у1=arcsin(sinx) и у2=, построен дополнительно еще один вспомогательный график: у3=-. От точек этого дополнительного графика (у3) отложены ординаты у1.

Кроме того, отмечены точки A и В, в которых графики функций у1 и у2 пересекаются, т. е. у=у1-y2=0; эти точки снесены на ось абсцисс.

15. y=—ax при а>1 (рис. 45).

Вспомогательные графики: y1= и у2=-ах. От точек кривой у2=-ах отложены ординаты у1=.

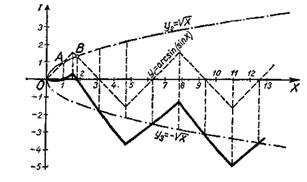
Рис. 44.

16. у=ах+а-х при а>1 (черт. 194). Вспомогательные графики: у1=ах и у2=а-х.

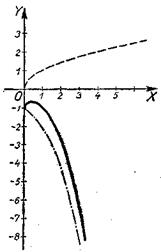
График заданной функции строится сложением ординат вспомогательных графиков: у=у1+у2.

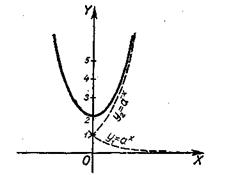
Рис. 45. Рис. 46.

При x=0 заданная функция имеет минимум: ymin=a0+a-0= 1+1=2.