График суммы и разности двух функций

Наиболее общий метод построения графиков суммы или разности двух функций заключается в том, что предварительно строятся (штриховыми линиями) два графика для обеих функций, входящих в сумму или разность, затем складываются или вычитаются ординаты этих кривых в характерных точках (пересечение кривых с осями координат, максимумы и минимумы, точки перегиба кривых и т.д.). По полученным точкам строится искомый график и производится проверка несколькими контрольными точками.

Если график суммарной функции имеет экстремум (максимум или минимум), то нахождение точки экстремума средствами элементарной математики возможно только при наличии каких-либо специальных средств заданной функции.

Упрощающие приемы построения графиков суммы и разности функций:

а) Если дана сумма функций, то строится график одной из них, более простой (например, линейной функции); затем к ней пристраивается график второй функции, ординаты которых откладываются от соответствующих точек первого графика.

б) Если задана разность функций, то строится (штриховой линией) график уменьшаемой функции и от нее откладываются ординаты вычитаемой функции, взятые с обратным знаком. Иногда удобно вычертить (штриховой линией) график вычитаемой функции с обратным знаком и ординаты обеих кривых (уменьшаемой функции и вычитаемой с обратным знаком) сложить.

в) Сумма или разность двух функций преобразовывается в одну функцию, если это возможно и если вычерчивание графика такой функции проще.

г) Построение графика алгебраической суммы функций упрощается, если использовать свойства четности, нечетности, периодичности и т.д.

Ниже приводятся примеры, иллюстрирующие как общий прием, так и упомянутые упрощающие приемы построения графиков суммы и разности двух функций.

1. у=х-sinx (рис. 31).

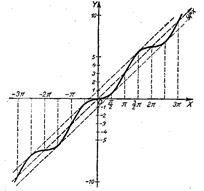
Рис. 31.

Имеем две функции: y1=x и у2=-sinx.

Строим график первой функции, затем от него (а не от оси х-ов) откладываем ординаты второй функции. Для облегчения построения параллельно прямой у1=х проведены две вспомогательные прямые: у=х+1 и у=x-1 На этих прямых находятся вершины синусоиды.

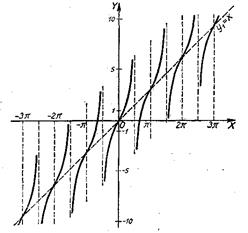
2. y=x+tgx (рис. 32).

Построение аналогично построению предыдущего графика.

y=x+lgx (рис. 33).

Строится прямая y1=x.

Характерные точки графика:

при х=1 y1=l; y=l+lgl=l; точка А(1;1);

при х=10 y1=10; y=10+lgl0=ll; точка В(10;11).

Из чертежа можно видеть, что область существования заданной функции (0; ¥), т. е. та же, что и для второго слагаемого у2=lgx.

у=х-arcsinx (рис. 34).

Заданная функция нечетная, так как

(-х)-arcsin(-х)=-х+arcsin х=-(x- arcsin x).

Поэтому построение можно выполнить только для правой части графика (при х ³ 0).