График суммы и разности двух функций

Найдем минимум данной функции.

Обозначим ax +a-x=k. (a)

Заметим, что:

область существования заданной функции: (-;), т. е. функция существует на всей числовой оси х-ов;

ах>0 и а-x>0 и, следовательно, k>0.

Преобразуем равенство (а):

ax+=k,

(б)

Так как ах ≠0, то равенство (б) равносильно равенству: a2x+1=axk, откуда получаем:

а2x-kax+1=0. (в)

Решаем уравнение (в) относительно ах:

(г)

Видим, что ах имеет действительное значение при ≥1, или k2≥4, т. е. |k|≥2.

А так как k>0, то |k|=k и, следовательно, k≥2. Таким образом, kmin=2, т. е.

(ax +a-x)min=2.

Подставляя в равенство (г) значение kmin, находим, что

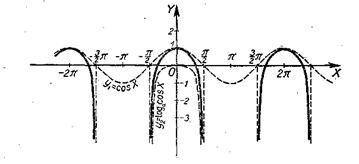Рис. 47

т.е. х=0.

17. y=logacosх+cosx (Рис. 47), где а>1.

Так как заданная функция периодическая, с периодом 2p, то построение проведено для одного периода: -.

Вспомогательные функции: y1=cosx и y2=logacosx.

Функция y1=cosx является внутренней для функции y2=logacosx, что учитывается при построении второго графика.

Граничные значения:

при х®(-) и х

y1=cosx®0 и y2=logacosх ®-∞; следовательно, у®-∞.

Характерная точка:

при х=0 у1=соsx=1; y2=logal=0; у=1, точка (0; 1).

При функция не определена, так как cosх≤0, и вспомогательная функция y2=logcosx не существует.

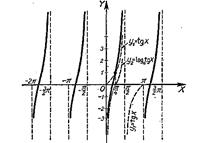
Рис. 48.

y=tgх+logatgх (рис. 48), где а>1.

Строится аналогично предыдущему графику.

Построение проведено, для одного периода (p): 0<х<p.

При функция не существует.

19. у=х+ (рис. 49).

Функция нечетная, так как

.

Построение графика проведено для х>0.

Вспомогательные графики: у1=х и у2=.

Прямая у1=х является асимптотой искомого графика.

Кроме того, при х>0 функция имеет минимум, который для функций данного вида может быть определен следующим образом.

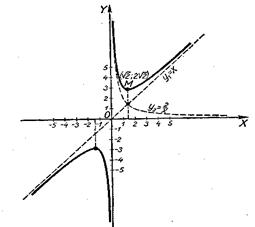
Рис. 49.

Возьмем функцию в общем виде: у=х+ при x>0.