Методика изучения площади геометрической фигуры

В методике работы над площадью фигуры имеется много общего с работой над длиной отрезка.

Прежде всего, площадь выделяется как свойство плоских предметов среди других их свойств. Уже дошкольники сравнивают предметы по площади и правильно устанавливают отношения "больше", "меньше", "равно", если сравниваемые предметы резко отличаются друг от друга или совершенно одинаковые. При этом дети пользуются наложением предметов или сравнивают их на глаз, сопоставляя предметы по занимаемому месту на столе, на земле, на листе бумаги и т.п. однако, сравнивая предметы, у которых форма различна, а различие площадей не очень четко выражено, дети испытывают затруднения. В этом случае они заменяют сравнение по площади сравнением по длине или по ширине предметов, т.е. переходят на линейную протяженность, особенно в тех случаях, когда по одному из измерений предметы сильно отличаются друг от друга.

В процессе изучения геометрического материала в I – II классах у детей уточняются представления о площади как о свойстве плоских геометрических фигур. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади. Этому способствуют упражнения на вырезание фигур из бумаги, черчение и раскрашивание их в тетрадях и т.п. В процессе решения задач с геометрическим содержанием учащиеся знакомятся с некоторыми свойствами площади. Они убеждаются, что площадь не изменяется при изменении положения фигуры на плоскости (фигура не становится ни больше, ни меньше). Дети многократно наблюдают соотношение между всей фигурой и ее частями (часть меньше целого), упражняются в составлении различных по форме фигур из одних и тех же заданных частей (т.е. построение равносоставленных фигур). Учащиеся постепенно накапливают представления о делении фигур на неравные равные части, сравнивая наложением полученные части, сравнивая наложением полученные части. Все эти знания и умения дети приобретают практическим путем попутно с изучением самих фигур.

Ознакомление с площадью можно провести так:

"Посмотрите на фигуры, прикрепленные к доске, и скажите, какая из них занимает больше всего места на доске (квадрат AMKD занимает места больше всех фигур). В этом случае говорят, что площадь квадрата больше, чем площадь каждого треугольника и квадрата CDMB. Сравните площадь треугольника АВС и квадрата AMKD (площадь треугольника меньше, чем площадь квадрата).

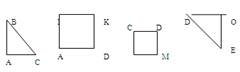
Эти фигуры сравниваются наложением – треугольник занимает только часть квадрата, значит, действительно площадь его меньше площади квадрата. Сравните на глаз площадь треугольника ФВС и площадь треугольника DOE (у них площади одинаковые, они занимают одинаковое место на доске, хотя расположены по-разному). Проверьте наложением.

Аналогично сравниваются по площади другие фигуры, а также предметы окружающей обстановки.

Однако не всегда так легко установить, какая из двух фигур имеет большую (меньшую) площадь или они одинаковы по площади. Чтобы показать это учащимся, можно предложить им сравнить вырезанные из бумаги прямоугольник и квадрат, незначительно отличающиеся по площади, например: размеры квадрата 4х4 дм, а прямоугольника 5х3 дм, при этом фигуры с обратной стороны разбиты на квадратные дециметры. Сначала учащиеся пытаются сравнить эти фигуры на глаз, а также путем наложения. Однако оба способа не помогают детям решить вопрос убедительно. Выслушав различные предположения, учитель поворачивает фигуры той стороной, на которой сделана разбивка на квадраты, и предлагает сосчитать, сколько одинаковых квадратов содержит каждая фигура. На этой основе дети устанавливают, площадь какой фигуры больше, а какой меньше. Аналогичные упражнения на сравнивание площади фигур, составленных из одинаковых квадратов, выполняются по учебнику, а также по чертежам, данным на доске. Дети убеждаются в том, что если фигуры состоят из одинаковых квадратов, то площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратов. Полезно на этом же уроке рассмотреть такой случай, когда разные по форме фигуры имеют одинаковую площадь, так как содержат одинаковое число квадратов. На последующих уроках включаются упражнения на подсчет квадратов, содержащихся в заданных фигурах, предлагается начертить в тетрадях фигуры, которые состоят из заданного числа квадратов (клеточек тетради). В процессе таких упражнений начинает формироваться понятие о площади как о числе квадратных единиц, содержащихся в геометрической фигуре.