График функции

Пример 10. Для построения графика функции y=f(х) некто составил таблицу значений аргумента и функции:

x	-2	-1	0	1	2
y	-1	0	1	2	3

Соответствующие пять точек показаны на рис. 5. На основании расположения этих точек он сделал вывод,

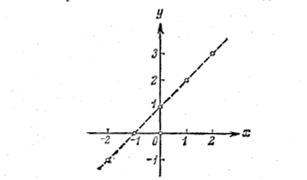Рис. 5.

что график функции представляет собой прямую (показанную на рис. 5 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. Простой пример иллюстрирует сказанное. Рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 6). Другим примером может служить функция y=x+1+sinpx; ее значения тоже описываются приведенной выше таблицей.

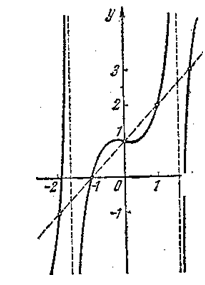Этот пример показывает, что в «чистом» виде метод построения графика по нескольким точкам ненадежен.

Рис. 6.

Поэтому для построения графика заданной функции, как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим в §4, а сейчас разберем некоторые часто применяемые способы построения графиков.

Основные свойства функции п.1.5.1. ограниченность

Теперь мы должны ознакомиться со свойством функций, которое является интегральным, т. е. может быть определено сразу для любого множества значений независимой переменной, не нуждаясь в предварительном определении для отдельных её значений (в отдельных точках). Функция у=f(х) называется ограниченной на множестве M, если все значения, принимаемые ею на этом множестве, принадлежат некоторому отрезку; очевидно, вместо этого мы можем предъявить и совершенно равносильное требование: существует такое положительное число с, что f(х)<с для всех хÎМ. Более детально, мы называем функцию у ограниченной сверху (снизу) на М, если существует такое число с, что f(х)<с (f(х)>с) для всех хÎМ. Функция просто ограниченная должна быть для этого, очевидно, ограничена как сверху, так и снизу.