График функции

Функция у=f(х) называется четной, если она обладает следующими двумя свойствами: 1) область определения этой функции симметрична относительно точки 0 (т.е. если точка а принадлежит области определения, то точка -а также принадлежит области определения); 2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство f(x)=f(-x).

Функция у=f(х) называется нечетной, если:

область определения этой функции симметрична относительно точки 0;

2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство f(x)=-f(-x).

Без труда проверяется, что функция y=|х| является четной. Точно так же функция у=х2n четна, а функция у=x2n+1 нечетна (при любом целом п). Без труда проверяется также, что сумма, разность, произведение и частное двух четных функций снова являются четными функциями. Далее, сумма и разность двух нечетных функций являются нечетными функциями. Наконец, произведение и частное двух нечетных функций являются четными функциями, а произведение и частное четной и нечетной функций являются нечетными функциями

Из сказанного следует, например, что многочлен, у которого все показатели четны, является четной функцией, а многочлен, у которого все показатели нечетны, является нечетной функцией. Так, функция y=х4+2х2-1 четна, а функция х3-х5 нечетна.

Не следует думать, что всякая функция непременно является или четной или нечетной: существуют функции, не являющиеся ни четными, ни нечетными.

Пример 15. Доказать, что функция f(х)=2х+1 не является ни четной, ни нечетной.

Решение. Областью определения этой функции является вся числовая ось, т. е. условие 1) в определении четной и нечетной функций выполнено. Чтобы доказать, что функция f(х), не является четной, мы должны поэтому доказать, что условие 2) в определении четной функции не выполнено, т. е. что существует (хотя бы одно) значение х, для которого f(x)f(-x). Возьмем x=1. Тогда f(1)=3, f(-1)=-1, т.е. f(1)¹f(-1). Таким образом, функция f(х) не является четной. Аналогично, так как f(1)¹-f(-1), то функция f(x)=2x+1 не является нечетной.

Четность или нечетность функции весьма существенно сказывается на форме графика этой функции. Именно, имеют место следующие две теоремы:

Теорема. График четной функции симметричен относительно оси у.

Доказательство. Пусть точка (x0; y0) принадлежит графику четной функции у=f(х), т.е. у0=f(х0). Точка, симметричная с точкой у=f(х) относительно оси у, имеет координаты (-х0; у0). Надо доказать, что точка (-x0; y0) принадлежит графику функции у=f(х), т.е. доказать, что y0 =f(-х0). Но это следует из определения четной функции: f(-х0)=f(х0)=y0.

Теорема. График нечетной функции симметричен относительно начала координат (0; 0).

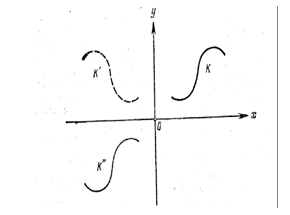
Замечание. Из этих теорем следует, что для построения графика четной функции достаточно построить часть графика этой функции для х³0, а затем построенную часть графика симметрично отразить относительно оси у, т.е. для каждой точки графика с абсциссой х>0 построить точку, симметричную ей относительно оси у. В частности, таким способом можно построить график функции y=f(|x|), так как функция f(|x|) является четной. Для построения графика нечетной функции достаточно построить часть графика этой функции для х³0, а затем построенную часть графика симметрично отразить относительно точки (0; 0), т.е. для каждой точки графика с абсциссой х>0 построить точку, симметричную ей относительно начала координат. (Заметим, что для осуществления симметрии некоторой кривой относительно начала координат можно поступить следующим образом: сначала данную кривую К симметрично отразить относительно оси ординат, а затем полученную кривую К' симметрично отразить относительно оси абсцисс, рис. 10)