График функции

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х, а на оси ординат - значения функции у=f(х). Графиком функции у=f(х) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции y=f(x).

Другими словами, график функции у=f(х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y=f(x).

Рис. 3.

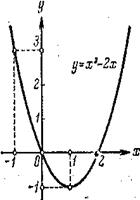
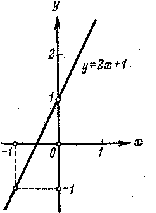
Рис. 2.

На рис. 2 и 3 приведены графики функций у=2x+1 и у=х2-2х.

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его куска, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х=а принадлежит области определения функции y=f(x), то для нахождения числа f(а) (т. е. значения функции в точке х=а) следует поступить так. Нужно через точку с абсциссой x=а провести прямую, параллельную оси ординат; эта прямая пересечет график функции у=f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 4). Например, для функции f(х)=х2-2х

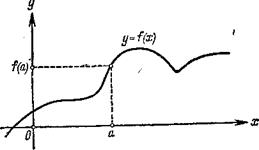
Рис. 4.

с помощью графика (рис. 3) находим f(-1)=3, f(0)=0, f(1)=-1, f(2)=0 и т.д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 3 ясно, что функция y=х2-2х принимает положительные значения при х<0 и при x>2, отрицательные - при 0<х<2; наименьшее значение функция у=х2-2х принимает при х=1.

Для построения графика функции f(х) нужно найти все точки плоскости, координаты х, у которых удовлетворяют уравнению у=f(х). В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно - с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений - скажем, x1, х2, ., хk - и составляют таблицу, в которую входят выбранные значения функции. Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции у=f(х). Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y=f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле, поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.