Методические разработки уроков по теме «Обратные тригонометрические функции»

2. Развивающая:

– развитие творческой активности и самостоятельности, находчивости;

3. Воспитательная

воспитание усидчивости, аккуратности.

Ход урока

I. Организационный момент:

– приветствие класса;

– проверить готовность класса к уроку;

– сообщить тему урока и цели.

II. Актуализация базовых знаний.

Фронтальный опрос.

1. Дать определение арксинуса, назвать область определения и значений функции, схематично изобразить на доске график.

2. Дать определение арккосинуса, назвать область определения и значений функции, схематично изобразить на доске график.

3. Какими свойствами они обладают?

III. Закрепление изученного материала через практику (учащиеся работают у доски).

Искомый график y = arcsin (sin |x–p/4|) получается из него сдвигом на p/4 вправо вдоль оси абсцисс (изображен сплошной линией на рис. 17) .

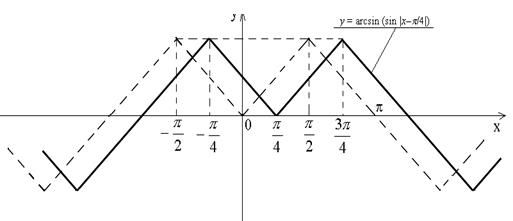
Рис. 17

IV. Упражнения на нахождение обратной функции и решение нестандартных задач по теме

Найти обратную функцию f –1 к функции f(x) = sin x, если а) D(f)= 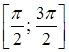; б) D(f)= .

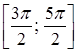Решение:

В обоих этих случаях функция f осуществляет взаимно однозначное соответствие между D(f) и E(f) =. Значит, обратная функция существует. В случае а) D (f -1) = ; E (f -1)= 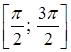. Для явной записи обратной функции решим уравнение sin x=у при условии 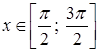. Так как arcsin у = =arcsin (sin x) = π–x (см. рис. 14), то х = π–arcsin у. Итак, в случае а) обратная функция (после обозначения аргумента ее через х, а самой обратной функции через у) задается формулой у = π–arcsin х.

В случае б), когда х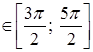, arcsin у = arcsin (sin x) = х-2π (см. рис. 14), т.е. х = 2π+arcsin у. Обратная функция задается формулой у = 2π + arc – sin х [19].

Найти обратную функцию к следующим функциям:

а) y=sin x на 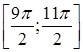; б) y=sin x на 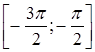; в) y=cos x на .

Решение:

а) Функция y = sin x осуществляет взаимно однозначное соответствие между D(f)= 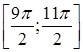и E(f)= . Значит, обратная функция существует. Для явной записи обратной функции решим уравнение sin x=y при условии 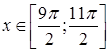. Так как на этом отрезке arcsin (sin x) = 5p – x, то arcsin y= =arcsin (sin x) = 5p–x, откуда y = 5p–arcsin x (явная запись обратной функции).

б) Аналогично примеру а), arcsin y = arcsin (sin x) = –p–x, откуда y = –p– arcsin x.

в) Аналогично примеру а), arccos y = arccos (cos x) = 4p +x, откуда x= =arccos y – 4p. Переобозначая х и у, имеем у = arccos х –4p.

Сравнить числа и .

Решение:

Заметим, что 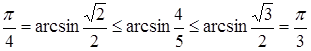и .

Углы близки. Попробуем вычислить значения тригонометрических функций упятеренного аргумента, так как значения их для известны. При этом . Удобнее вычислить , т. к. его значения по разные стороны от имеют разные знаки.

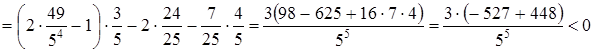
3-ей четверти, а потому