Методические разработки уроков по теме «Обратные тригонометрические функции»

Aрккосинусом числа а, если |а|1, называют угол, косинус которого принадлежит отрезку; его обозначают arccos а.

Таким образом, arccos а есть угол, удовлетворяющий следующим двум условиям: сos (arccos a) = a, |а|1; 0 ≤ arccos a ≤ π.

Например, arccos, так как cos и; arccos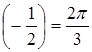, так как cosи .

Функция y=arccos x (рис. 15) определена на отрезке, областью ее значений является отрезок. На отрезке функция y = arccos x непрерывна и монотонно убывает от π до 0 (поскольку y = cos х – непрерывная и монотонно убывающая функция на отрезке ); на концах отрезка она достигает экстремальных значений: arccos(–1)= π, arccos 1 = 0. Отметим, что arccos 0 = .

График функции y = arccos x (см. рис. 15) симметричен графику функции y = cos x относительно прямой y = x .

Рис. 15

Покажем, что имеет место равенство arccos(–x) = π – arccos x.

В самом деле, по определению 0 ≤ arccos х ≤ π. Умножая на (–1) все части последнего двойного неравенства, получаем –π ≤ arcсos х ≤ 0. Прибавляя π ко всем частям последнего неравенства, находим, что 0 ≤ π – arccos х ≤ π. Таким образом, значения углов arccos(–х) и π–arccos х принадлежат одному и тому же отрезку. Поскольку на отрезке косинус монотонно убывает, то на нем не может быть двух различных углов, имеющих равные косинусы. Найдем косинусы углов arccos(–х) и π–arccos х. По определению cos (arc – cos x)= – x, по формулам приведения и по определению cos (π–arccos х) =-cos (arccos х) = – х. Итак, косинусы углов равны, значит, равны и сами углы.

При выполняется равенство arccos (cos x) = х. Так как функция четна, то мы можем построить ее график на отрезке . Затем воспользуемся периодичностью функции с периодом 2π. График функции изображен на рисунке 16.

Рис. 16

III. Домашнее задание.

Рассмотреть и проработать основные положения по изученному материалу, а именно:

– выучить определения функций арксинус и арккосинус, их свойства, вид графиков;

– изучить способ вычисления значений аркфункций.

IV. Подведение итогов.

Итак, давайте вспомним, что сегодня мы узнали (учитель с помощью учащихся):

– что такое система арксинус, арккосинус;

– какими свойствами они обладают;

– как можно найти значения аркфункции и построить ее график.

Конспект урока по алгебре №2 (10 класс)

Тема урока:

Обратные тригонометрические функции. Арксинус и арккосинус.

Тип урока: закрепление изученного материала.

Методы обучения: наглядный, словесный, практический.

Средства обучения: доска, конспект лекций, задачник, методические указания.

Цели урока:

1. Образовательная:

– закрепить тему «Обратные тригонометрические функции. Арксинус и арккосинус»;

– выработать умения производить различные действия над арксинусом и арккосинусом, строить графики.