Методические разработки уроков по теме «Обратные тригонометрические функции»

Если есть, то учитель ещё раз повторяет непонятные положения.

Конспект урока по алгебре №4 (10 класс)

Тема урока:

Обратные тригонометрические функции. Арктангенс и арккотангенс.

Тип урока: обобщение и систематизация знаний.

Методы обучения: наглядный, словесный, практический.

Средства обучения: доска, конспект лекций, задачник, методические указания.

Цели урока:

1. Образовательная:

– обобщить и систематизировать знания и умения по изучаемой теме;

– повторить и закрепить пройденный материал.

2. Развивающая:

– развитие самостоятельности, интеллекта и воли учащихся.

3. Воспитательная

– прививать интерес к математике;

– воспитание целеустремленности и аккуратности.

Ход урока

I. Организационный момент:

– приветствие класса;

– проверить готовность класса к уроку;

– сообщить тему урока и цели.

II. Актуализация базовых знаний

Фронтальный опрос.

1. Дать определение арктангенса, назвать область определения и значений функции, схематично изобразить на доске график.

2. Дать определение арккотангенса, назвать область определения и значений функции, схематично изобразить на доске график.

3. Какими свойствами они обладают?

III. Упражнения (предполагается, что ученики решают самостоятельно у доски, но под контролем учителя).

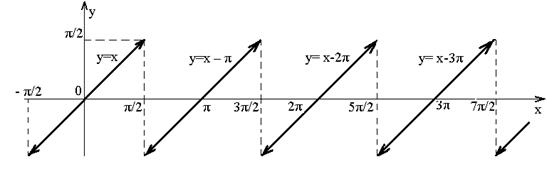
Рис. 19

Найти arctg (tg p2).

Решение:

Так как 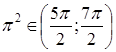, можем выполнить следующие преобразования: аrctg (tg p2) = аrctg (tg(3p + (p 2–3p))) = |воспользуемся формулами приведения|= аrctg (tg(p2–3p)), где уже p2–3p 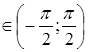, тогда arctg (tg p2) = =аrctg (tg(p 2–3p) = p2–3p [16].

Найти наибольшее значение

(sin11x) + и х, при которых оно достигается.

Решение:

(sin11x) Поэтому(sin11x)+ , при этом , если .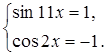

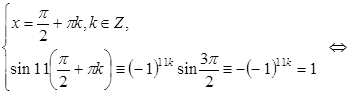
Ответ: 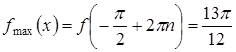[19].

IV. Подведение итогов.

Ребята, на этом уроке мы выполнили нелегкую задачу. Мы закрепили изученный нами материал, а также разобрались в непонятных вопросах. Но может, что-нибудь непонятное в этой теме все же осталось?

Если да, то учитель помогает учащимся до конца разобраться в данной теме.

Данный урок нацелен на повторение ключевых вопросов. Задания на этом уроке являются более сложными. Поэтому целесообразно подробно обсуждать ход решения каждой задачи, предлагать учащимся давать объяснения своих выводов. Если возможен не один способ решения упражнения, необходимо найти и обсудить их все.