Изучение основных элементарных функций в школьном курсе математики

В 10 классе в учебнике Алимова рассматривается показательная функция. Основная цель –познакомить с многообразием свойств и графиков показательной функции в зависимости от значений оснований и показателей степени.

Первое с чем знакомятся ученики на уроках математики – это свойства показательной функции и ее графиком. На ее изучение отводится один параграф, который начинается с повторения свойств степеней. После чего вводится определение показательной функции. Далее рассматриваются основные свойства показательной функции. Свойства монотонности обосновываются аналитически и иллюстрируются на графике. В дальнейшем основное внимание уделяется иллюстрации свойств функции по графику (чтение графика). Приводятся примеры применения показательной функции для описания различных физических процессов. В учебнике приводится в пример формула радиоактивного распада 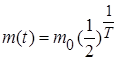, где m(t) и mo – масса радиоактивного вещества соответственно в момент времени t и в начальный момент времени t=0, T - период полураспада (промежуток времени, за который первоначальное количество вещества уменьшится вдвое). Так же рассказывается, что с помощью показательной функции выражается давление воздуха в зависимости от высоты подъема, ток самоиндукции в катушке после включения постоянного напряжения.

В учебниках Колмогорова показательная функция изучается в 11 классе. Прежде чем ввести понятие показательной функции f(x)=ax, где х принимает любые значения из множества действительных чисел, проводится подготовительная работа. Начинается со знакомства учащихся с функцией f(x)=ax, область определения которой – множество рациональных чисел. Для каждого положительного числа а можно найти значение выражения ( - любое рациональное число). Таким образом, любому числу х из множества Q соответствует действительное число ax. На странице 179-180 учебника после определения показательной функции помещен материал, адресованный учащимся, проявляющим повышенный интерес к занятиям математикой. В нем описана схема доказательства существования значения показательной функции для любого иррационального х (следовательно, и самой функции).

В учебнике Мордковича учащиеся впервые сталкиваются с понятием показательной функции уже в 9 классе, на примере формулы п-го члена геометрической прогрессии. Следующая встреча с данной функцией у учащихся происходит только в 11 классе. В §45 сначала рассматривается функция у=2х, хÎQ. При рассмотрении свойств у=2х отмечается, что это возрастающая функция, неограниченная сверху и ограниченная снизу, не имеющая ни наименьшего, ни наибольшего значения.

Кроме того, рассматривается функция у=2х при х=. Доказывается, что при вычислении получается конкретное число. То есть в учебнике Мордковича рассматриваются функции не только с рациональным показателем, но и действительным.

При формулировке общих свойств графика функции, рассматриваются два случая, когда основание целое число и дробное число большее нуля, но меньшее единицы. И только после этого вводится определение показательной функции.

Кроме того, в учебнике Мордковича изучается горизонтальная асимптота графика функции, и способ ее отыскания.

В учебнике обращается внимание на то, что учащиеся иногда путают понятия показательной функции и стенной. Предлагается сравнить данные функции. Далее автор не забывает упомянуть функцию . Говорится, что данная функция не считается ни показательной, ни степенной, но ее иногда называют показательно- степенной.